
భారతీయ గణితి మేధావి శ్రీనివాస రామానుజం
గ్రీకు భాషనుంచి వచ్చిన Mathematics పదానికి అర్ధం: విజ్ఞాన శాస్త్రం, జ్ఞానం మరియు నేర్చుకొనుట - ఇంకా వివరణలోనికి వెళితే- సంఖ్యలు (numbers), వాటి రూపం, వాటి గణనం, బీజగణితము (Algebra), రేఖాగణితం (geometry), త్రికోణమితి (trigonometry), కలన గణితం(Calculus) వాటి విశ్లేషణ మున్నగునవి. గణితశాస్త్రం, ఆధునిక దైనందిన జీవనంలో ఎంత అవసరమో మనందరికీ తెలుసు. లెక్కలు వాడకుండా ప్రస్తుత పరిస్థితులలో ఒక్క అడుగు పడదు, రోజు గడవదు, వ్యాపార ఆలోచన ముందుకి సాగదు. అంకెలు అనాదిగా వాడుకలో ఉన్నప్పటికీ, వాటిని క్రమబద్దీకరణ చేసి వాటిలో ముఖ్యంగా శున్యాన్ని గుర్తించి దానిని వాడుకలోకి తెచ్చినది మాత్రం భాస్కరాచార్య II. ఆర్యభట్ట బీజగణితాన్ని క్రీ.శ. 500 లో బోధిస్తే, అనేక ఆచార్యులు (శ్రీపతి, లీలావతి, నారాయణ, జ్ఞానరాజా, గణేశ మున్నగు వారు) వివిధ శాస్త్ర రంగాలలోను గణితశాస్త్రము దాని ఉపయోగాన్ని, వాడే విధానాన్ని విశదీకరించి దాని వాడుక సామర్ధ్యాన్ని పెంచారు. బౌధాయనుడు, ‘పైథాగరస్’ పుట్టడానికి రెండు మూడు శతాబ్దాలముందే ముందే- ఇప్పుడు ‘పైథాగరస్’ సిద్ధాంతంగా చెప్పబడుతున్న సిద్ధాంతాన్నే- 'సులభసుత్రాల' లో ఉదాహరించి (1-58 & 1-59) వాటిని వాడుకలోనికి తెచ్చి అనేక క్రతువులు, యజ్ఞ యాగాదులకు ఉపయోగించే గుండాల నిర్మాణంలోనూ, పెద్ద కోటలు, రాజభవనాల నిర్మాణ విధానంలో వాడేవారు. ఆర్యభట్ట 'పై (π అనగా 22 /7' యొక్క విలువ 3 .1416 గా క్రీ.శ. 499 లోనే నిర్ణయించి ఉపయోగించి చూపాడు. సుమారు క్రీ పూ ఆరు-ఏడు శతాబ్దాలకు చెందిన బౌధాయనుడు కృష్ణ యజుర్వేద విభాగమైన తైత్తిరీయము లో తన ఆరు సూత్రాల (శ్రౌత, కర్మ, ద్వైధ, గ్రిహ్య, ధర్మ, సులభ) ద్వారా, దానిలో ప్రత్యేకంగా సులభ సూత్రాలలో ప్రస్తుతం పైథాగొరస్ సిద్ధాంతం గా పిలవబడుతున్న దానిని, రెండు యొక్క వర్గమూలం మొదలైన వాటిని విశదీకరించాడు. వాటిని ఆ రోజులలో వైదిక శాస్త్ర నిర్మాణావసరాలకి, కర్మ కాండలకు, ఇతర భవన నిర్మాణావసరాలకు వాటిని ఉపయోగించేవారు. ఆ సూత్రం లో ఏ విధంగా చెప్పబడిందంటే,
'దీర్ఘచతురస్రస్యాక్షణ్యయా రజ్జుః పార్శ్వమాని తిర్యగ్మాని చ యత్పృధగ్భూతే కురుతాస్తదుభయం కరోతి'.
అనగా, ఒక దీర్ఘచతురస్రంలోని వికర్ణం (ఒక తాడు తో కొలిస్తే) యొక్క చతురస్ర విస్తీర్ణం మిగిలిన రెండు భుజాల మొత్తం చతురస్ర విస్తీర్ణాలతోటి సమానం. అల్లాగే ఒక చతురస్ర వైశాల్యం వృత్త వైశాల్యానికి ఏవిధంగా సమానమవుతుందో, లేక వృత్త వైశాల్యం చతురస్ర వైశాల్యానికి సమానం చెయ్యొచ్చో సూత్రం i.58 లో నిరూపించాడు. అల్లాగే సూత్రం i.61.2 లో 2 యొక్క వర్గమూలాన్ని- అనగా√2= 1.414216 ఏవిధంగా సాధించవచ్చునో నిరూపించాడు.
 ఈ భారతీయ గణితశాస్త్ర పరంపరావృద్ధిని కొనసాగించడానికా అన్నట్లు శ్రీనివాస రామానుజం 1887 డిసెంబర్ 22న తమిళనాడులోని ‘ఈరోడ్’ లో బీదకుటుంబీకుడైన శ్రీ శ్రీనివాస అయ్యంగారికి, శ్రీమతి కోమలత అమ్మాళ్ కి ఏకైక పుత్రునిగా జన్మించాడు. కానీ వారి బీదరికం సరైన పోషకవిలువలుగల ఆహారాన్ని ఇవ్వలేక అతడిని తరుచు అనారోగ్యానికి గురిచేస్తుండేది. కాని, కుటుంబ ఆర్ధిక నిమ్నత అతని మనోవికాసానికి గాని మేధాశక్తి సామర్ధ్యాల సహజాభివృద్ధికి గాని అడ్డుపడలేదు. మొదటినుంచి తన ప్రతిభ తో తరగతి లో మొదటి శ్రేణి లోనే నిలచేవాడట. అతని 15 వ ఏట 'జార్జ్ షూబ్రిడ్జి కార్' యొక్క "సినోప్సిస్ అఫ్ ఎలిమెంటరీ రిజల్ట్స్ ఇన్ ప్యూర్ అండ్ అప్లైడ్ మ్యాథమెటిక్స్" అనే గణిత శాస్త్ర పుస్తకం ఒక స్నేహితుని ద్వారా సంపాదించిన తరువాత దానిలో పూర్తిగా నిమగ్నుడై దానిలోని వెయ్యి పైగా ఉన్న సిద్ధాంతాలని క్షుణంగా పరిశీలించడమే కాకుండా, కొన్ని అసంపూర్ణంగా ఉన్న నిరూపణలని స్వయం కృషితో పూర్తిచెయ్యడమేకాకుండా, అదే త్రోవలో కొత్త సిద్ధాంతాలని రూపొందించి వాటి నిరూపణ విధానాన్ని చూపించి మదరాసు విశ్వవిద్యాలయం యొక్క గణితశాస్త్ర పరిశోధనా పారితోషికాన్ని సంపాదించాడు. ఆ పుస్తకం అతని దృక్పధాన్ని మొత్తం గణితంవైపు ఆకర్షించి, అతడి బుద్ధికౌశలం పై పెను సవాళ్ళను విసిరి అతడి దానిని పెంచి గణితంలో పురోభివృద్ధి సాధించే టట్లు చేయ గలిగినా తక్కిన విషయాలపై గల ఆసక్తిని క్రమంగా నిర్వీర్యపరచి, అతడు ఉద్యోగార్థిగా ఎదుర్కొన్న పోటీపరీక్షలల్లో అపజయాన్నే చవిచూపించింది. ఆ విధంగా అది అతనిని గణిత శాస్త్రంలో ఉన్నత శిఖరాలు ఎక్కించినా, సామాన్యజీవనంలో అసహాయుణ్ణి చేసి అతడి ఆర్ధిక ఔన్నత్యానికి కుటుంబం సాఫీగా సాగడానికి నోచుకోకుండా చేసింది.
ఈ భారతీయ గణితశాస్త్ర పరంపరావృద్ధిని కొనసాగించడానికా అన్నట్లు శ్రీనివాస రామానుజం 1887 డిసెంబర్ 22న తమిళనాడులోని ‘ఈరోడ్’ లో బీదకుటుంబీకుడైన శ్రీ శ్రీనివాస అయ్యంగారికి, శ్రీమతి కోమలత అమ్మాళ్ కి ఏకైక పుత్రునిగా జన్మించాడు. కానీ వారి బీదరికం సరైన పోషకవిలువలుగల ఆహారాన్ని ఇవ్వలేక అతడిని తరుచు అనారోగ్యానికి గురిచేస్తుండేది. కాని, కుటుంబ ఆర్ధిక నిమ్నత అతని మనోవికాసానికి గాని మేధాశక్తి సామర్ధ్యాల సహజాభివృద్ధికి గాని అడ్డుపడలేదు. మొదటినుంచి తన ప్రతిభ తో తరగతి లో మొదటి శ్రేణి లోనే నిలచేవాడట. అతని 15 వ ఏట 'జార్జ్ షూబ్రిడ్జి కార్' యొక్క "సినోప్సిస్ అఫ్ ఎలిమెంటరీ రిజల్ట్స్ ఇన్ ప్యూర్ అండ్ అప్లైడ్ మ్యాథమెటిక్స్" అనే గణిత శాస్త్ర పుస్తకం ఒక స్నేహితుని ద్వారా సంపాదించిన తరువాత దానిలో పూర్తిగా నిమగ్నుడై దానిలోని వెయ్యి పైగా ఉన్న సిద్ధాంతాలని క్షుణంగా పరిశీలించడమే కాకుండా, కొన్ని అసంపూర్ణంగా ఉన్న నిరూపణలని స్వయం కృషితో పూర్తిచెయ్యడమేకాకుండా, అదే త్రోవలో కొత్త సిద్ధాంతాలని రూపొందించి వాటి నిరూపణ విధానాన్ని చూపించి మదరాసు విశ్వవిద్యాలయం యొక్క గణితశాస్త్ర పరిశోధనా పారితోషికాన్ని సంపాదించాడు. ఆ పుస్తకం అతని దృక్పధాన్ని మొత్తం గణితంవైపు ఆకర్షించి, అతడి బుద్ధికౌశలం పై పెను సవాళ్ళను విసిరి అతడి దానిని పెంచి గణితంలో పురోభివృద్ధి సాధించే టట్లు చేయ గలిగినా తక్కిన విషయాలపై గల ఆసక్తిని క్రమంగా నిర్వీర్యపరచి, అతడు ఉద్యోగార్థిగా ఎదుర్కొన్న పోటీపరీక్షలల్లో అపజయాన్నే చవిచూపించింది. ఆ విధంగా అది అతనిని గణిత శాస్త్రంలో ఉన్నత శిఖరాలు ఎక్కించినా, సామాన్యజీవనంలో అసహాయుణ్ణి చేసి అతడి ఆర్ధిక ఔన్నత్యానికి కుటుంబం సాఫీగా సాగడానికి నోచుకోకుండా చేసింది.
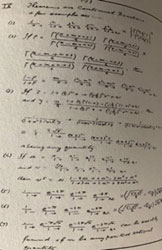
 1909 లో రామానుజం పదేళ్ల జానకి అమ్మాళ్ తో వివాహమైన తరువాత బాధ్యతలు పెరిగి, ధనార్జన తమ పొట్టలు నింపుకోవడానికి అవసరమని గ్రహించినవాడై ఉద్యోగప్రయత్నాలు తీవ్రతరం చేసాడు. ఆ సందర్భాల్లోనే ప్రభుత్వాధికారి రామచంద్ర రావుని ఇంటర్వ్యూ ద్వారా కలవడం జరిగింది. 1911 లో అతని మొదటి పరిశోధనా పత్రం 'జర్నల్ అఫ్ ఇండియన్ మాథెమటికల్ సొసైటీ' లో ప్రచురించబడింది. కాని అతడి చెప్పేవిధానం, అనుసరించిన తర్కం, మిగిల్చిన కొద్దీ ఆధారాలు దాని సంపూర్ణ అవగాహనకి సహాయపడక, అది చాలామంది గణితశాస్రజ్ఞుల మెప్పును పొందలేకపోయింది. కాని రామచంద్ర రావు ద్వారా లభించిన పారితోషికం ఆయన పరిశోధనావసర రొక్కాన్ని సమకూర్చగలిగినా అది వారివురి అవసరాలకి సరిపోక ఆర్ధిక ఇబ్బందులలో మునిగి తేలుతుండేవాడు. మార్చ్ 1912 లో 'మద్రాస్ పోర్ట్ ట్రస్ట్' లో గుమస్తాగా చేరి, ఆర్ధిక స్థితి మెరుగు పడినా వీలు దొరికినప్పుడల్లా అతని మొదటి ఆసక్తి అయిన గణితశాస్త్ర పరిశోధనకై కాలాన్ని వినియోగిస్తుండేవాడు. మదరాసు పోర్ట్ లో ముఖ్య అకౌంటెంట్ గా ఉంటున్న ఎస్. నారాయణ అయ్యర్, ఇండియన్ మాథెమటికల్ సొసైటీ కోశాధికారి అవడం మరియు సర్ ఫ్రాన్సిస్ స్ప్రింగ్ పోర్ట్ ట్రస్ట్ ఇంజినీర్ & పోర్ట్ ట్రస్ట్ అధ్యక్షుడు, mathematical Society కి కూడా అధ్యక్షుడు కావడం, వారివురు రామానుజం మేధాశక్తి, గణిత శాస్త్ర ప్రవీణ్యతకి అబ్బురపడి, అతడిని బ్రిటిష్ ప్రొఫెసర్స్ కి పరిచయం చెయ్యాలని చాలా ప్రయత్నించి, చివరికి ప్రొఫెసర్ గోడ్ఫ్రెయి హెరాల్డ్ హార్డీ అనే ప్రసిద్ధ గణిత శాస్త్రజ్ఞుడికి లేఖలద్వారా పరిచయం చేసారు. రామానుజం జనవరి 1913 లో హార్డీ కి తొమ్మిది పేజీల పరిశోధన పత్రాలు పంపిస్తూ (తొమ్మిదవ పేజీ నకలు ప్రక్క పటంలో చూడొచ్చు) వ్రాసిన లేఖని హార్డీ, తన మిత్రుడు, కేంబ్రిడ్జి విశ్వవిద్యాలయంలో గణిత శాస్త్రజ్ఞుడైన జె ఈ. లిటిల్వుడ్ కి పరిశీలనార్థం చూపి, పిమ్మట ఆ యిద్దరు చర్చించుకుని రామానుజం గొప్ప మేధావిగా నిర్ణయించుకుని రామానుజాన్ని కేంబ్రిడ్జి విశ్వవిద్యాలయానికి ఆహ్వానించారు. ఆ తొమ్మిది పేజీలలోని సూత్రాలు ఈనాటికి గొప్ప విశ్లేషణాత్మక విషయాలుగా 'జర్నల్ అఫ్ ది లండన్ మాథెమటికల్ సొసైటీ' లో చర్చించబడుతున్నాయంటే వాటియొక్క ప్రగాఢత చెప్పకనే చెబుతున్నాయి. కాని అప్పటి సాంఘిక ఆచార పద్ధతులననుసరించి సముద్రం దాటివెడితే కుల బహిష్కరణని ఎదుర్కోవాలనే నియమానికి వెనుకాడి మదరాసు లోనే వారిరువురి సహకారంతో కేంబ్రిడ్జి విశ్వవిద్యాలయం వారి సహాయంతో మదరాసు విశ్వవిద్యాలయంలోనే రెండేళ్లు పరిశోధన సాగించాడు. ఆ సమయంలో హార్డీ అతని స్నేహితుడైన తన విద్యార్థి, రామానుజం వయస్సు వాడే అయిన - ఎరిక్ హెరాల్డ్ నెవిల్ల్ ని- 1914 జనవరి లో మదరాసు విశ్వవిద్యాలయంలో గణిత శాస్త్రంలో 21 ఉపన్యాసాలు ఇచ్చే మిషతో రామానురాజాన్ని ఒప్పించి కేంబ్రిడ్జి రావడానికి అంగీకరింపచెయ్యడంకోసం పంపించాడు. నెవిల్ల్ తో జరిగిన మూడవ సమావేశంలో రామానుజం అంతవరకూ ఎవ్వెరికి చూపని తన పరిశోధనా నోట్స్ చూపించి ఆ పుస్తకాన్ని అవసరమనుకుంటే తీసుకుని వెళ్లవచ్చునని చెప్పాడట. దానిలో అతని గణిత పరిశోధనా వివరాలన్నీ ఉన్నాయి. అవి పరిశీలించిన నెవిల్ల్ గణిత శాస్త్రంలో రామానుజానికి గణితంలో గల జ్ఞాన విస్తృతి చూసి ఆశ్చర్య చకితుడయ్యాడట. దానిని తరువాత హార్డీ కి వివరించాడని వేరే చెప్పక్కర్లేదు.
1909 లో రామానుజం పదేళ్ల జానకి అమ్మాళ్ తో వివాహమైన తరువాత బాధ్యతలు పెరిగి, ధనార్జన తమ పొట్టలు నింపుకోవడానికి అవసరమని గ్రహించినవాడై ఉద్యోగప్రయత్నాలు తీవ్రతరం చేసాడు. ఆ సందర్భాల్లోనే ప్రభుత్వాధికారి రామచంద్ర రావుని ఇంటర్వ్యూ ద్వారా కలవడం జరిగింది. 1911 లో అతని మొదటి పరిశోధనా పత్రం 'జర్నల్ అఫ్ ఇండియన్ మాథెమటికల్ సొసైటీ' లో ప్రచురించబడింది. కాని అతడి చెప్పేవిధానం, అనుసరించిన తర్కం, మిగిల్చిన కొద్దీ ఆధారాలు దాని సంపూర్ణ అవగాహనకి సహాయపడక, అది చాలామంది గణితశాస్రజ్ఞుల మెప్పును పొందలేకపోయింది. కాని రామచంద్ర రావు ద్వారా లభించిన పారితోషికం ఆయన పరిశోధనావసర రొక్కాన్ని సమకూర్చగలిగినా అది వారివురి అవసరాలకి సరిపోక ఆర్ధిక ఇబ్బందులలో మునిగి తేలుతుండేవాడు. మార్చ్ 1912 లో 'మద్రాస్ పోర్ట్ ట్రస్ట్' లో గుమస్తాగా చేరి, ఆర్ధిక స్థితి మెరుగు పడినా వీలు దొరికినప్పుడల్లా అతని మొదటి ఆసక్తి అయిన గణితశాస్త్ర పరిశోధనకై కాలాన్ని వినియోగిస్తుండేవాడు. మదరాసు పోర్ట్ లో ముఖ్య అకౌంటెంట్ గా ఉంటున్న ఎస్. నారాయణ అయ్యర్, ఇండియన్ మాథెమటికల్ సొసైటీ కోశాధికారి అవడం మరియు సర్ ఫ్రాన్సిస్ స్ప్రింగ్ పోర్ట్ ట్రస్ట్ ఇంజినీర్ & పోర్ట్ ట్రస్ట్ అధ్యక్షుడు, mathematical Society కి కూడా అధ్యక్షుడు కావడం, వారివురు రామానుజం మేధాశక్తి, గణిత శాస్త్ర ప్రవీణ్యతకి అబ్బురపడి, అతడిని బ్రిటిష్ ప్రొఫెసర్స్ కి పరిచయం చెయ్యాలని చాలా ప్రయత్నించి, చివరికి ప్రొఫెసర్ గోడ్ఫ్రెయి హెరాల్డ్ హార్డీ అనే ప్రసిద్ధ గణిత శాస్త్రజ్ఞుడికి లేఖలద్వారా పరిచయం చేసారు. రామానుజం జనవరి 1913 లో హార్డీ కి తొమ్మిది పేజీల పరిశోధన పత్రాలు పంపిస్తూ (తొమ్మిదవ పేజీ నకలు ప్రక్క పటంలో చూడొచ్చు) వ్రాసిన లేఖని హార్డీ, తన మిత్రుడు, కేంబ్రిడ్జి విశ్వవిద్యాలయంలో గణిత శాస్త్రజ్ఞుడైన జె ఈ. లిటిల్వుడ్ కి పరిశీలనార్థం చూపి, పిమ్మట ఆ యిద్దరు చర్చించుకుని రామానుజం గొప్ప మేధావిగా నిర్ణయించుకుని రామానుజాన్ని కేంబ్రిడ్జి విశ్వవిద్యాలయానికి ఆహ్వానించారు. ఆ తొమ్మిది పేజీలలోని సూత్రాలు ఈనాటికి గొప్ప విశ్లేషణాత్మక విషయాలుగా 'జర్నల్ అఫ్ ది లండన్ మాథెమటికల్ సొసైటీ' లో చర్చించబడుతున్నాయంటే వాటియొక్క ప్రగాఢత చెప్పకనే చెబుతున్నాయి. కాని అప్పటి సాంఘిక ఆచార పద్ధతులననుసరించి సముద్రం దాటివెడితే కుల బహిష్కరణని ఎదుర్కోవాలనే నియమానికి వెనుకాడి మదరాసు లోనే వారిరువురి సహకారంతో కేంబ్రిడ్జి విశ్వవిద్యాలయం వారి సహాయంతో మదరాసు విశ్వవిద్యాలయంలోనే రెండేళ్లు పరిశోధన సాగించాడు. ఆ సమయంలో హార్డీ అతని స్నేహితుడైన తన విద్యార్థి, రామానుజం వయస్సు వాడే అయిన - ఎరిక్ హెరాల్డ్ నెవిల్ల్ ని- 1914 జనవరి లో మదరాసు విశ్వవిద్యాలయంలో గణిత శాస్త్రంలో 21 ఉపన్యాసాలు ఇచ్చే మిషతో రామానురాజాన్ని ఒప్పించి కేంబ్రిడ్జి రావడానికి అంగీకరింపచెయ్యడంకోసం పంపించాడు. నెవిల్ల్ తో జరిగిన మూడవ సమావేశంలో రామానుజం అంతవరకూ ఎవ్వెరికి చూపని తన పరిశోధనా నోట్స్ చూపించి ఆ పుస్తకాన్ని అవసరమనుకుంటే తీసుకుని వెళ్లవచ్చునని చెప్పాడట. దానిలో అతని గణిత పరిశోధనా వివరాలన్నీ ఉన్నాయి. అవి పరిశీలించిన నెవిల్ల్ గణిత శాస్త్రంలో రామానుజానికి గణితంలో గల జ్ఞాన విస్తృతి చూసి ఆశ్చర్య చకితుడయ్యాడట. దానిని తరువాత హార్డీ కి వివరించాడని వేరే చెప్పక్కర్లేదు.
 ఒకనాడు అతడి తల్లి వారి కులదైవమైన 'నామగిరి అమ్మన్' దర్శించుకు రమ్మని ఆదేశించగా, అతని స్నేహితుడు నారాయణ అయ్యర్ తో మూడు రోజులు ఆ ఆలయంలోనే గడిపారు. మూడోరాత్రి రామానుజానికి నిద్రలో దేవి దర్శనమిచ్చి విదేశంలో విద్యార్జన చెయ్యమని ఆదేశించిందట. అప్పుడు రామానుజం తల్లి అనుజ్ఞ తో కేంబ్రిడ్జి విశ్వవిద్యాలయం వారి పునరాహ్వానంపై మార్చ్ 17, 1914 ప్రొద్దుట 10 ఘంటలకి మదరాసు లో బయలుదేరిన 'నేవాస' అనే పేరు గల ఓడ శ్రీ లంకలోని కొలంబో మీదుగా ఏప్రిల్ 14 న లండన్ చేరింది. అతని భార్య రామానుజంతో తనని కూడా లండన్ తీసుకెళ్లమని కోరిందిట. కాని తాను వెడుతున్న లక్ష్యానికి అక్కడ ఆమె ఉనికి అడ్డుగా నిలుస్తుందని, ఆమె కోరికని తిరస్కరించాడట.
ఒకనాడు అతడి తల్లి వారి కులదైవమైన 'నామగిరి అమ్మన్' దర్శించుకు రమ్మని ఆదేశించగా, అతని స్నేహితుడు నారాయణ అయ్యర్ తో మూడు రోజులు ఆ ఆలయంలోనే గడిపారు. మూడోరాత్రి రామానుజానికి నిద్రలో దేవి దర్శనమిచ్చి విదేశంలో విద్యార్జన చెయ్యమని ఆదేశించిందట. అప్పుడు రామానుజం తల్లి అనుజ్ఞ తో కేంబ్రిడ్జి విశ్వవిద్యాలయం వారి పునరాహ్వానంపై మార్చ్ 17, 1914 ప్రొద్దుట 10 ఘంటలకి మదరాసు లో బయలుదేరిన 'నేవాస' అనే పేరు గల ఓడ శ్రీ లంకలోని కొలంబో మీదుగా ఏప్రిల్ 14 న లండన్ చేరింది. అతని భార్య రామానుజంతో తనని కూడా లండన్ తీసుకెళ్లమని కోరిందిట. కాని తాను వెడుతున్న లక్ష్యానికి అక్కడ ఆమె ఉనికి అడ్డుగా నిలుస్తుందని, ఆమె కోరికని తిరస్కరించాడట.
ప్రొఫెసర్ బ్రూస్ బెర్న్, ఒక ప్రసిద్ధ గణాంక విశ్లేషకుడు దశాబ్దాలు రామానుజం నోట్స్ ని క్షుణంగా పరిశీలించి చాలా పుస్తకాలు ప్రచురించాడు. వాటిలో చాలా భాగం సరిఐయినవే అని ఉద్ఘాటించాడు.
రామానుజం కి కేంబ్రిడ్జి లో వచ్చే పారితోషికం అతడి అక్కడి అవసరాలకే కాకుండా ఇండియా లోని కుటుంబ అవసరాలకి కూడా సరిపోయి అక్కడ ఉన్న మొదటి మూడు సంవత్సరాలు చాలా సంతోషంగా బాగుగానే గడిచింది. ఆ కాలంలోనే అతడు అత్యుత్తమ ఉత్పాదక సాధించగలిగాడు. అప్పుడు జానకి అమ్మాళ్ అతడి తలిదండ్రుల వద్ద ఉంటూ అతడికి ఎటువంటి చీకుచింత లేకుండా చేసింది.
రామానుజం ఇంగ్లాడులో ఉన్న కొద్దీ కాలంలోనే దాదాపు 4000 రుజువులు (proofs), గుర్తింపులు (Identities), సంజాయిష్కరణలు (Conjuctures), సమీకరణాలు (equations) స్వచ్ఛ గణితం (Pure Mathematics) లో సాధించాడు.
అతడి 'తీటాఫంక్షన్' భౌతిక శాస్త్రం ‘స్టింగ్ థియరీ’ కి హృదయం వంటిది.
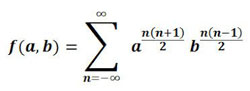
జగత్తులోని అన్ని మౌలిక భాగాలు, మనకి కణాలు గా కనిపించే పదార్ధాలు నిజానికి వివిధ తీగల పౌనః పున్య నిర్దుష్ట ప్రకంపనాలు మాత్రమే అన్నదే దాని వాదన.
అతడు సాధించిన మరికొన్ని గణిత శాస్త్ర నిర్ధారణలు
Ramanujam-Soldner Constant: μ=1.4513692349. (సుమారు) as seen on logarithmic integral function.
Landau-Ramanujan Constant: లండావు నియమంలో రామానుజం నిర్ధారించిన మరొక స్థిరం.
రామానుజం సంకలనం:
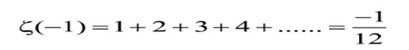
ఒకసారి, హార్డీ క్షయ తో బాధ పడుతున్న రామానుజాన్ని చూడడానికి వస్తూ 'నేను 1729 నంబర్ గలటాక్సీలో వచ్చాను, అది చాలా అశుభమైనది గా అని పిస్తోంది' అని అంటే, వెంటనే రామానుజం 'కానే కాదు, అది చాలా ఆసక్తికరమైన సంఖ్య. అది రెండు అతి చిన్న ఘనాల మొత్తం రెండు వేర్వేరు పద్దతులలో వ్యక్తపరుస్తే.' అన్నాడు.
అనగా 1729 = 13 +123 = 93+103. 7x13x19 కూడా. దీన్ని 'రామానుజం నంబర్' అని కూడా పిలుస్తారు.
ఈ వ్యాఖ్య హార్డీ ని ఆశ్చర్య పరచడమే కాదు, ఆహ్లాదాన్ని కూడా కలిగించింది.
ఇవి రామానుజం శోధించి సాధించిన అనేక గణిత శాస్త్ర అద్భుత పరిశోధనలలో కొన్ని మాత్రమే.
సరదాకి అతడు చూపిన ఈ క్రింది సంఖ్య అమరిక చూడండి:
1 x 8 + 1 = 9.
12 x 8 + 2 = 98
123 x 8 + 3 = 987.
1234 x 8 + 4 = 9876.
12345 x 8 + 5 = 98765.
123456 x 8 + 6 = 987654
1234567 x 8 + 7 = 9876543.
12345678 x 8 + 8 = 98765432.
123456789 x 8 + 9 = 987654321.
1 x 9 + 2 = 11
12 x 9 + 3 = 111
123 x 9 + 4 = 1111
1234 x 9 + 5 = 11111
12345 x 9 + 6 = 111111
123456 x 9 + 7 = 1111111
1234567 x 9 + 8 = 11111111
12345678 x 9 + 9 = 111111111
123456789 x 9 +10= 1111111111.
And Look At This Symmetry
9 x 9 + 7 = 88
98 x 9 + 6 = 888
987 x 9 + 5 = 8888.
9876 x 9 + 4 = 88888
98765 x 9 + 3 = 888888
987654 x 9 + 2 = 8888888
9876543 x 9 + 1 = 88888888
98765432 x 9 + 0 = 888888888
1 x 1 = 1
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321
కాని అక్కడి చలికాలంలో అతడు ఊహించని విపరీత శీతల వాతావరణం, విటమిన్ల లోపం వల్ల అతడి శరీరం అనారోగ్యానికి గురి అయింది. అది క్రమంగా 1917 కి క్షయ వ్యాధిగా ముదిరి అతడు చాలాకాలం శానిటరియంల లోను, నర్సింగ్ హోమ్ లోను గడప వలసి వచ్చింది.
ఆరోగ్యం కొంచం బాగుపడ్డాక 1919 ఫిబ్రవరి నెలలో మదరాసు తిరిగి వచ్చేసాడు. వచ్చిన తరువాత దురదృష్టవశాత్తు, అట్టేరోజులు జీవించి ఉండలేదు. అతడు ఆరోజుల్లో మదరాసు లో తాగిన నీటి లోని కాలేయాన్ని నాశనంచేసే పరాన్నజీవులు అతడిని బలిగొనగా 32 వ ఏట అనగా 1920 ఏప్రిల్ 26 న తుదిశ్వాస విడిచాడు. ఒక భారతీయ గణిత శాస్త్ర పురోగమనాధ్యానికి ఆ క్రమాన అనుకోనివిధంగా తెరపడింది. కాకతాళీయంగా ఆదిశంకరులు కూడా 32 సంవత్సరాలే జీవించారు.
రామానుజం సంతకం:

 రామానుజం మే 2 1918 న 31 వ ఏట "ఫెలో అఫ్ రాయల్ సొసైటీ' గా రెండవ భారతీయునిగాను, 13 అక్టోబర్ 1918 న 'ఫెలో అఫ్ ట్రినిటీ కాలేజీ', కేంబ్రిడ్జి మొదటి భారతీయుడిగాను ఎన్నిక అయి అతడి అసాధారణ మేధాశక్తి కి, కాలేజీ శిక్షణా రహిత గణిత శాస్త్ర విద్యాభ్యాసానికి, ఆర్జించిన విజ్ఞానానికి, గుర్తింపు లభించింది. స్వయం కృషితో గణిత శాస్త్రంలో ప్రావీణ్యత సాధించి విశ్లేషక సంఖ్యా సిద్ధాంతం (Analytical Theory of numbers), దీర్ఘవృత్తాకార విధులు (Elliptic Functions), కొనసాగే భిన్న సంఖ్యలు (Continued Fractions), అనంత శ్రేణి (Infinite Series) ల పరిశోధనలో గణనీయ శిఖరాలని సాధించగలిగాడు, రామానుజం.
రామానుజం మే 2 1918 న 31 వ ఏట "ఫెలో అఫ్ రాయల్ సొసైటీ' గా రెండవ భారతీయునిగాను, 13 అక్టోబర్ 1918 న 'ఫెలో అఫ్ ట్రినిటీ కాలేజీ', కేంబ్రిడ్జి మొదటి భారతీయుడిగాను ఎన్నిక అయి అతడి అసాధారణ మేధాశక్తి కి, కాలేజీ శిక్షణా రహిత గణిత శాస్త్ర విద్యాభ్యాసానికి, ఆర్జించిన విజ్ఞానానికి, గుర్తింపు లభించింది. స్వయం కృషితో గణిత శాస్త్రంలో ప్రావీణ్యత సాధించి విశ్లేషక సంఖ్యా సిద్ధాంతం (Analytical Theory of numbers), దీర్ఘవృత్తాకార విధులు (Elliptic Functions), కొనసాగే భిన్న సంఖ్యలు (Continued Fractions), అనంత శ్రేణి (Infinite Series) ల పరిశోధనలో గణనీయ శిఖరాలని సాధించగలిగాడు, రామానుజం.
ఏ కాలేజిలోను గణితశాస్త్రం పద్దతిగా చదువుకోని రామానుజం కీర్తి శేషుడైన ఒక శతాబ్దం తరువాత కూడా నేటికీ అతడు వ్రాసుకున్న నోట్స్ పై పరిశోధన జరుగుతూనే ఉంది, పరిశోధించిన గణిత శాస్త్ర నిపుణులు వాటి రుజువులు సాధించి, వాటి సార్ధకత నిరూపిస్తూనే ఉన్నారు. అయినా ఇంకా నిరూపించవలసినవి చాలానే ఉన్నాయి.
-o0o-
Note: Most the information is obtained from internet and some also from the book “The man who knew Infinity” by Robert Kanigel, published by Washington Square Press
very nice article onRamanujam
Thank you
గొప్ప గణిత వేత్త గూర్చి చాలా విలువైన సమాచారం అందించారు.ధన్యవాదాలు
Thank you. మీకు నచ్చినందుకు సంతోషం